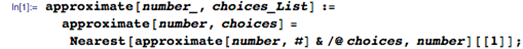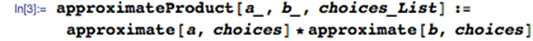Wolfram 分析 | 12乘法表有什么意义吗？

2022-10-25 12:29发布

站内文章 / 软件
343 0 0

我的政府（我在英国）最近（2013年6月26日原稿发布）说，这里的孩子应该在 9 岁之前学习到 12 乘法表。现在，我一直相信，我之所以学习 12 乘法表，是因为英国过去的货币制度——一先令等于12 便士。这种疯狂在我出生后的第二年以十进制结束，到 1970 年代后期，如果不得不学习12 乘法表，似乎就已经变成毫无意义地浪费时间了。

1024-011.png


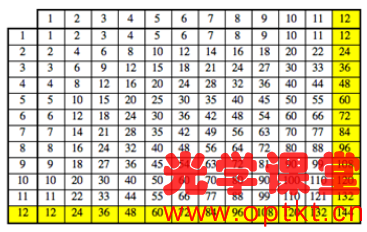
近 40 年后发现它得到了新的重视，这让我感到很奇怪，以至于我想我应该从数学上多研究一点。这是我得出的结论。

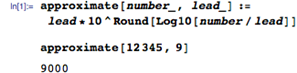
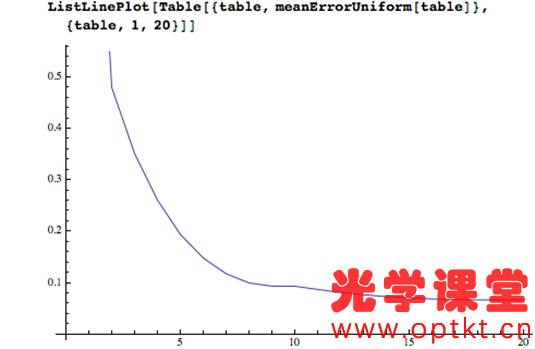
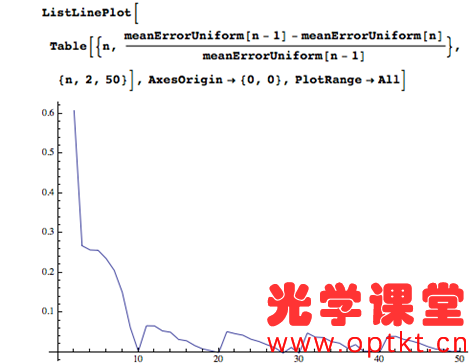
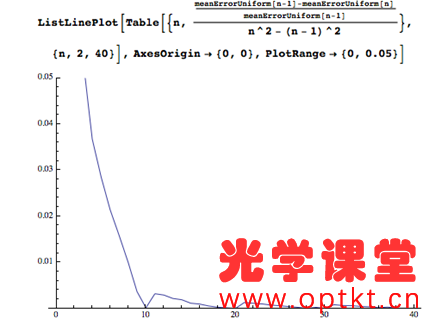
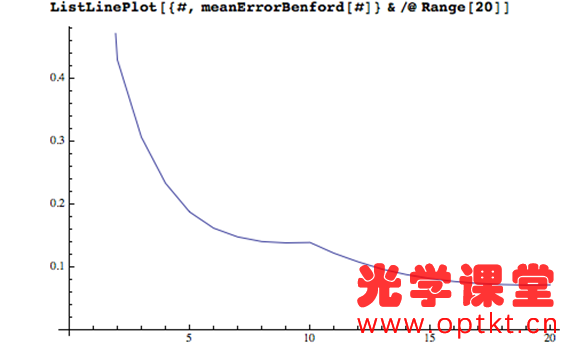
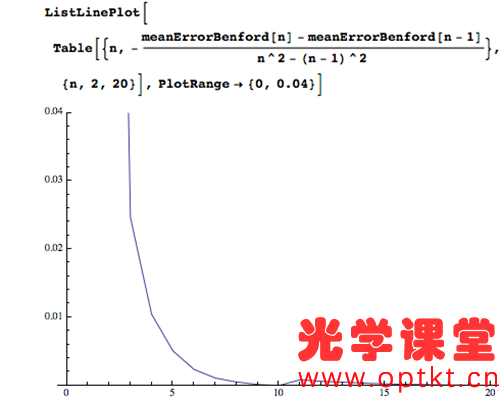
让我们从一个基本问题开始：究竟为什么我们要使用乘法表？

我将声称有三个基本原因：

  • 1) 直接知道常见乘法题的答案。

  • 2) 启用乘法算法。

  • 3) 使近似乘法成为可能。

让我们依次看看这些原因。
1

这个原因很重要。日常生活中有很多小的乘法问题，毫无疑问知道这些问题的答案是有用的。但是知道任何问题的任何答案都是有用的。1 乘以 12 有什么特别之处？为什么停在 12 乘法表上——为什么不学习 13、14、15、16 和 17 乘法表？为什么不学习 39 乘法表？随着表格数量的增加，学习量随着数字的平方而增加，而遇到使用该表格的问题的共性会下降。“知道”所有可能问题的答案是一项艰巨的任务，不值得付出努力。毕竟，这就是发明数学的原因，这样我们就不会必须知道所有可能计算的答案，而是在需要时有办法解决它们。我们必须在某处画一条线，然后转向更算法化的方法。问题是这条线应该画在哪里。



2

有很多花哨的计算算法，但我们大多数人都学习“列乘法”，这涉及一次对一个数字进行运算，同时管理数字位置并将溢出带到下一列。我自己有时仍然使用它。根据定义，它需要 0-9 乘法表（并隐含理解 10 倍表），因为它一次只需要一位数字，但任何一位数字都可以出现。11 和 12 乘法表的知识完全无关紧要。如果这是唯一的考虑因素，那么在 10 乘法表上，我们有明确的论据来划清界限。您不能管理更少，而更多是没有用的。



3

但是还有另一种有用的算法，它是将数字近似为几个有效数字。这可能是将线画得更高的理由。



以 7,203 x 6,892 为例。如果我想确切地知道这个结果，那么我会使用 Mathematica（或者如果我绝对必须这样做，我会使用铅笔和纸在列中应用乘法）。但通常我只需要一个粗略的答案，所以我在心里将其转换为 7,000 x 7,000 = 7 x 7 x 1,000 x 1,000 = 49,000,000。更正式地，我将数字转换为 k x 10 n 形式的最接近的近似值，其中 k ∈ { 我知道乘法表的数字集}。然后我在剩余的有效数字上使用乘法表，并隐式地使用 10 乘法表来获得正确的幅度。在这种情况下，真正的答案是：





7203 × 6892



49643076





有 1.2% 的误差——对于许多应用来说已经足够了。现在，如果我知道72 乘法表，我可以得到这个 7,200 x 6,900 = 49,680,000。只有 0.07% 的误差。

所以，现在我们的“我在哪里画线”的问题变成了“如果我最多知道 12 乘法表，与只知道10乘法表相比，典型的近似计算要好多少？” 让我们调查一下。首先，我需要使用给定的引领数字执行近似过程。

1024-03.png


并将其扩展到寻找最佳近似值，如果我们可以选择引领数字。

1024-04.png


例如，如果我最多只知道我的 4 乘法表，那么 18,345 的最佳近似值是 20,000。

1024-05.png


现在我们的近似乘积只是每个数字的最佳近似值的乘积。

1024-06.png

并且可以从与准确答案相比的差异中找到相对误差。

1024-07.png

例如，计算 549 x 999 当您最多只知道 10 乘法表时，误差会超过8%。

1024-08.png

现在，让我们将“典型计算”视为涉及 1 到 100 万之间均匀分布数字的计算，并将“典型”误差视为 100,000 次此类计算的平均值。

1024-09.png

如果您知道最多 10 乘法表，典型误差是 9.4%。

1024-10.png

但如果您知道12 乘法表，典型误差只有 8.2%。

1024-11.png

这是学习乘法表数量与误差的函数。 

1024-12.png

有趣的是，大部分改进都是在您了解 7 乘法表时发生的。在10处出现奇怪突起是因为近似的能力依赖于已经知道的10乘表(以便能够处理末尾的零)。

我们可以计算出每额外学习一个乘法表，典型错误相对改进有多少。

1024-13.png

因此，相对收益以循环方式逐渐下降。

但是将错误率从 9% 提高到 8% 是有代价的。知道10乘表需要回忆 100 个事实（好吧，55，如果你假设对称）。但是知道 12 乘表是 144 个事实。将误差从结果的 9.3% 提高到 8.1%，相对误差大小提高了12%。但要实现这一点，您需要额外记住 40% 的信息。这似乎是一个失败的提议。

让我们看看每多记忆一个事实，对结果的相对改善。

1024-14.png

接近10乘表，“努力的回报”非常迅速地下降，然后几乎没有提高。在 10 时停止我们的死记硬背似乎是一个相当有说服力的案例。事实上，如果乘法表仅用于估计，我们将通过仅查看数量级并仅使用 1 和 10乘表来为每次努力获得最佳回报！

当然，数字不是均匀分布的。如果您从事鸡蛋生产，那么 6s 和 12s 可能会出现很多，就像您碰巧是前十进制英国硬币的经销商一样！像这样的上下文问题很难量化，但一个普遍的问题是Benford 定律，它出现在许多现实世界的数据集中。它表示，如果您查看涵盖多个数量级的真实数据集（例如社区人口、人们的债务或计算机上的文件大小），那么这些数字更有可能以 1 开头而不是 2 ，并且更有可能以 2 而非 3 开头，依此类推。我不知道有没有人研究过第二位数的分布，所以我假设这是统一的。所以这是一个生成“真实世界”数字的函数。

1024-15.png

我们现在可以对这些更现实的数字重复我们的分析。

1024-16.png

1024-17.png

使用这些不太统一的数字表现较差（使您更有可能需要准确的计算而不是近似值）。通过了解更多的表仍然可以实现改进，这可以作为学习超过 12 乘法表的论据，但当您考虑到每额外学习一个事实带来的回报时就不行了，这使得在学习10乘表后停止更有说服力。

1024-18.png

如果您真的想进行一些额外的死记硬背学习，那么有比学习 11 和 12 乘法表更好的方式来花费您的精力。学习 1 到 10 以及 15 和 25 的所有排列会比 1 到 12 乘法表产生更好的平均结果（因为它们更均匀地近似于前导数字为 1 或 2 的数字）。

1024-19.png

或者，正如 Chris Carlson 向我建议的那样，学习接近 100 的倒数（2 x 50 = 100、3 x 33 = 99、4 x 25 = 100、5 x 20 = 100、6 x 17 = 102 等），因为它们经常出现。我认为学习2的平方和幂可能也比学习11和12的乘法表更有用。

由于没有希望恢复之前十进制货币系统，我只能得出结论，这个新的优先级背后的逻辑很简单，“如果学习 10 乘法表是好的，那么学习到 12 乘法表就更好了。”当您想提高数学标准的时候，谁能反对呢? 除非您把数学应用到这个问题上!  


购买软件/免费试用【13.1.0中英文 Wolfram 软件】

可扫码申请

IMG_8531.JPG




赞赏支持

热门文章