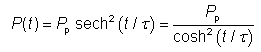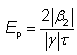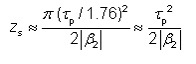本教程包含以下部分:
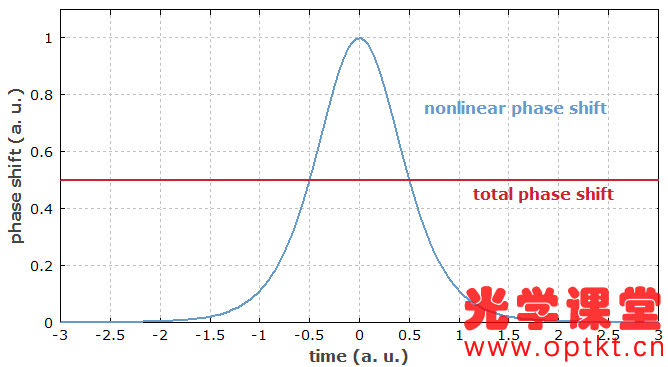
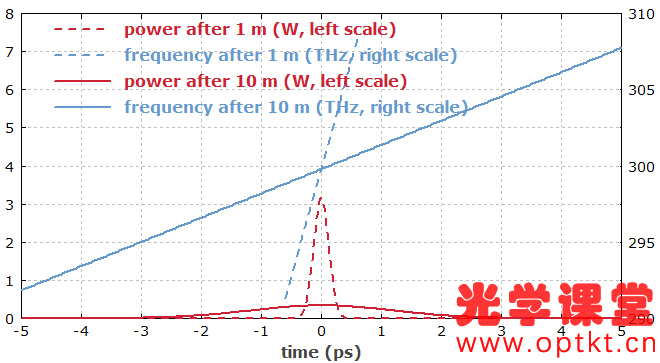
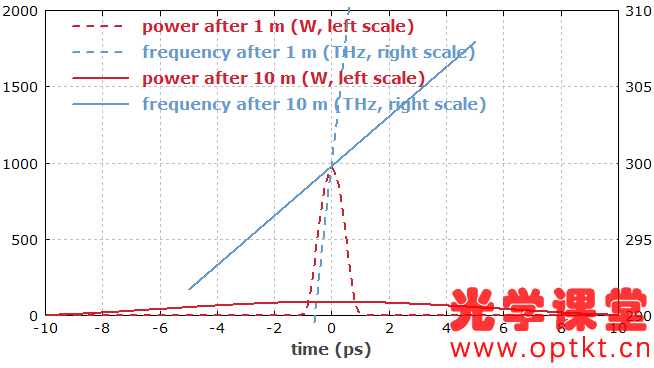
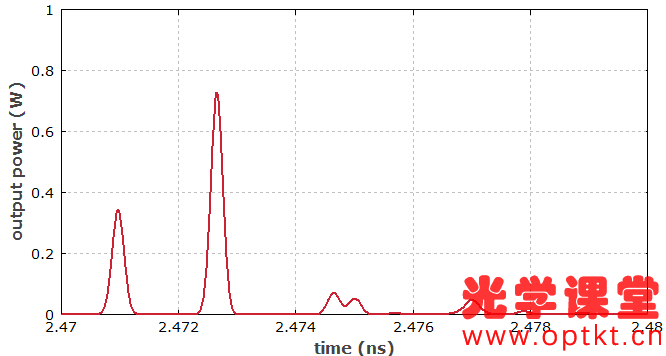
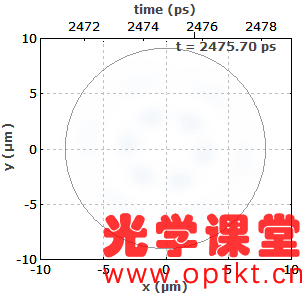
① 玻璃光纤中的导光 ② 光纤模式 ③ 单模光纤 ④ 多模光纤 ⑤ 光纤末端 ⑥ 光纤接头 ⑦ 传播损耗 ⑧ 光纤耦合器和分路器 ⑨ 偏振问题 ⑩ 光纤的色散 ⑪ 光纤的非线性特性 ⑫ 光纤中的超短脉冲和信号 ⑬ 光纤配件和工具 这是 Paschotta 博士的无源光纤教程的第 12 部分 第十二部分:光纤中的超短脉冲和信号 当超短脉冲(脉宽为皮秒或飞秒量级)在光纤中传播时,它们会经历脉宽和光谱变化,主要是由于色散(第 10 部分)和非线性效应(第 11 部分)。这里给出了重要影响的一些概述。 如果光峰值功率足够低,非线性效应可以忽略不计,但我们还是会考虑色散的影响。在本教程的第 10 部分中,我们已经讨论了色散的起源。在这里,我们看一下脉冲传输的一些后果。 超短脉冲的光谱带宽是有限的,即由不同的频率分量组成。色散的基本效应是这些频率分量以不同的群速度传播。如果它们都是因注入脉冲而聚集在一起(即我们注入一个“变换限制脉冲”,在给定带宽内脉宽可能最小),则更快的频率分量将在光纤端更快地出现,其次是比较慢的频率分量。对于正常色散(正群速度色散),较长波长的分量最快;然后可以观察到脉冲的向上啁啾,即瞬时频率上升。 例如,考虑能量为1 pJ,脉宽为100 fs和中心波长为1000 nm 的高斯形状的初始脉冲。该脉冲的带宽为 ≈0.44 / 100 fs = 4.4 THz(变换受限高斯脉冲的时间带宽积约为 0.44)。它被注入到单模光纤中,群速度色散为 10,000 fs 2 /m,则4.4 THz 的脉冲带宽对应于2 π · 4.4 THz · 10,000 fs 2 /m = 276 fs/m 的传输时间范围。因此,我们猜预计1米的光纤会出现明显的增宽。 一个有用的经验法则实际上是:如果总群延迟色散(群速度色散乘以光纤长度)达到脉冲持续时间的平方,则色散脉冲展宽将会很明显。对于非变换限制脉冲,光谱展宽更强。 计算脉冲展宽效应并不难: 对输入脉冲形状进行傅里叶变换。 根据色散应用与频率相关的相位变化:只需将每个频率分量的复振幅乘以exp( i ( β 2 /2) ( ω - ω 0 ) 2 ),其中β 2是群速度色散,ω 0频谱中心的角频率。 转换到时域,你就有了时域中的脉冲。根据需要绘制其功率、瞬时频率或其他与时间有关的变量。 当然,使用RP Fiber Power之类的软件工具来处理这些事情很方便;您只需要描述输入脉冲、光纤和您想要绘制的任何内容。图 1 显示了 1 m 和 10 m 光纤输出脉冲的功率和瞬时频率随时间的演变。 图 1: 1 m 和 10 m 光纤中 1-pJ 脉冲的光功率和瞬时频率。 可以看到脉冲的线性向上啁啾出现了,这两种情况都跨越了相同的频率范围——脉冲的光带宽。10 m 的光纤的啁啾斜率比1 m 光纤要低,因为在相同的频率范围会在更长的时间内被扫描。因此,如果啁啾以 GHz/ps 为单位量化,那么“色散越大,啁啾越大”的说法是完全错误的;只有在扩大进程开始时才会如此。 如果我们对 1 nJ 而不是 1 pJ 的脉冲能量进行相同的模拟,我们也会得到明显的非线性效应(这在数值上比较难模拟;一个典型的方法是使用分步傅里叶法)。自相位调制现在增加了光谱宽度,因此色散展宽比以前更强。图 2 给出了更宽的时间范围: 图 2:光纤经过1 m 和 10 m 后 具有1-nJ 脉冲的光功率和瞬时频率。在这里,非线性效应变得很重要。 光谱宽度现在从 4.4 THz (14.7 nm) 增加到 18.8 THz (62.7 nm)。 若非线性效应忽略不计,只需用相反符号的色散就很容易重新得到时间展宽。因此,可以通过将上啁啾脉冲发送到具有反常色散的光纤中或将下啁啾脉冲发送到具有正常色散的光纤中来获得色散脉冲压缩。若非线性效应不可忽略,原则上它们可以通过合适的色散分布进行补偿——然而,实践起来比较困难。因此,光纤作为脉冲压缩器在大多数情况下仅限于峰值功率相对较小的脉冲。此外,如果光谱恒定的二阶色散足够大,则脉冲压缩是最容易的,即光谱相位随着频率偏移的平方变化。 多模光纤还有另一种色散:模间色散。这意味着不同的模式(见第 2 部分)具有不同的群速度;我们已经在第 4 部分讨论了模间色散。如果将超短脉冲入射到光纤中,会使多个模式被激发,并且相应的模式到达输出端的时间是不相同的。 图 3 显示了输出功率与时间的关系,其中 200-fs 脉冲穿过 50 cm 的阶跃折射率光纤。输入脉冲的空间轮廓为高斯分布,但他并不是与光纤轴完全对齐。基模首先出现,因为它是最快的。大约 1.7 ps 之后是 LP 11 模式——实际上它是两种不同方向的模式的叠加。(这些模式是退化的,假设光纤是完全对称且保持直线。)之后会出现更多的模式。 图 3: 具有 200-fs 输入脉冲的光纤的输出功率与时间的关系。 图 4 将以动画图形的形式显示结果。可以很好地看到光纤如何将输入分解为模式,并在不同时间呈现这些模式。 图 4: 200-fs 输入脉冲的与时间相关的输出光束轮廓(动画图形)。动画图形是使用 RP Fiber Power 软件制作的。 很容易理解,模间色散可能会完全扰乱电信号。当他比较强时,发送符号需要的时间相当长,并且比特率相应地低。但是,可以通过使用具有抛物线折射率分布的渐变折射率光纤来最小化模间色散,如多模光纤的第 4 部分所示;这可以提高比特率。另一种可能是使用单模光纤,它不会有这种危害。所以对于长距离传输,仅需使用单模光纤。 我们已经看到,如果正常的色散和非线性(通常具有正的非线性指数)共同作用,使得时间脉冲展宽增加,并产生上啁啾脉冲。对于具有反常色散的光纤,即具有负群速度色散的光纤,其行为是完全不同的。在这里,色散往往会产生下啁啾,这可以抵消 SPM 产生的上啁啾。对于合适的脉冲形状和脉冲能量,甚至有可能色散效应和非线性效应完全相互抵消,使得时域或频域下的脉冲形状在传播过程中保持不变。(只有一个额外的整体相移,这通常与应用无关。)这样的脉冲称为基本孤子。 高阶色散可忽略不计的无损光纤中基本孤子脉冲传播的条件是该脉冲是无啁啾的 sech 2 脉冲 且脉冲能量 E p 和孤子脉冲持续时间 τ 满足以下条件: 这里,半峰全宽 (FWHM) 脉冲持续时间为 τ p ≈ 1.7627 × τ,γ 是以 rad / (W m) 为单位的 SPM 系数,β 2 是群速度色散,定义为对角频率的导数,即每单位长度的群延迟色散(以 s 2 /m 为单位)。 图 5: 对基本孤子脉冲的非线性和色散影响。蓝色曲线:仅与时间相关的非线性相移(无色散),与光强度成正比。红色曲线:由非线性和色散对孤子的共同作用引起的整体相移。 恒定相移不会改变脉冲在时域或频域里的形状。 如果脉冲能量是基本孤子的 N 2倍(其中 N 是整数),并且脉冲形状不变,则可以获得 N 阶的高阶孤子。在这里,时域或频域里的脉冲形状不是恒定的,而是以周期性方式演变,孤子周期为: 色散脉冲展宽和压缩
模间色散
反常色散和非线性的组合效应:孤子脉冲