本教程包含以下部分:
① 玻璃光纤中的导光
② 光纤模式
③ 单模光纤
④ 多模光纤
⑤ 光纤末端
⑥ 光纤接头
⑦ 传播损耗
⑧ 光纤耦合器和分路器
⑨ 偏振问题
⑩ 光纤的色散
⑪ 光纤的非线性
⑫ 光纤中的超短脉冲和信号
⑬ 附件和工具
这是 Paschotta 博士的无源光纤教程的第 6 部分
第六部分:光纤接头
纤维接头的类型
光纤可以连接在一起,从而使光有效地从一根光纤传输到另一根光纤。有多种可能性:
机械拼接是指通过一些机械手段将两个光纤末端紧紧地固定在一起。这通常用于永久连接,但也可以在不损坏光纤末端的情况下拆除接头。
另一种技术是熔接,其中纤维熔接在一起,例如使用电弧。如果两个光纤纤芯相似,这会导致插入损耗特别低,回波损耗特别高。
对于非永久性连接,也可以使用光纤连接器(见下文)。

图 1:光子晶体光纤( PCF,左侧)和传统光纤(右侧) 之间熔接的显微镜想象。可以看到 PCF 的孔图案。照片由 NKT Photonics 友情提供。
不完美光纤接头的耦合损耗
一个常见问题是耦合损耗有多大,例如在机械接头处,当存在某种缺陷时,例如:
纤芯的平行偏移,
纤维轴方向之间的偏差,
核心尺寸不匹配,或
光纤末端之间的气隙。
事实证明,对于单模和多模光纤,有些答案是完全不同的。
单模光纤
计算单模光纤的耦合损耗相对容易。本质上,来自第一根光纤(输入)的导模在第二根光纤中产生了一些幅度分布,这可能会有些位移,例如,由于不完美的拼接。现在可以将耦合效率计算为该幅度分布与第二根光纤的导模之间的重叠积分。(不需要数值光束传播。)
对于具有不同模式半径和一些平行偏移的高斯模式轮廓的情况,可以使用我们在第 3 部分中已经讨论过的方程:
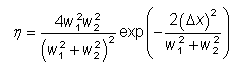
类似的方程可用于角度失配:
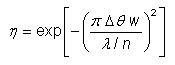
这表明角度对准对于具有大模式面积的单模光纤更为关键。对于标准模式区域,角度对齐通常比位置对齐更容易实现。
下图基于上述等式。
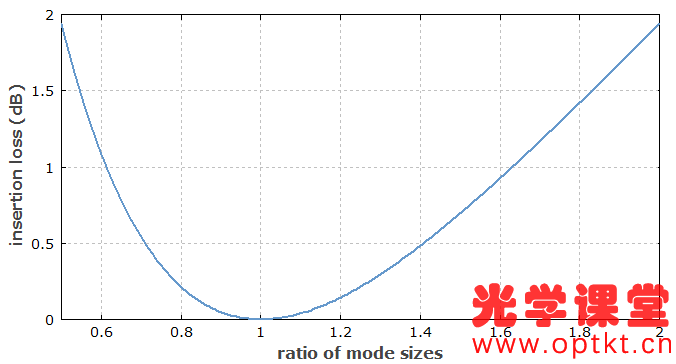
图 2: 由于模式半径不匹配导致的单模光纤机械接头处的插入损耗。
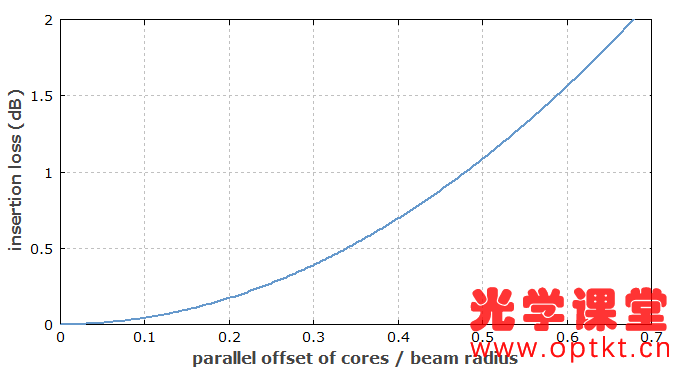
图3:由于纤芯平行偏移,单模光纤机械接头处的插入损耗。
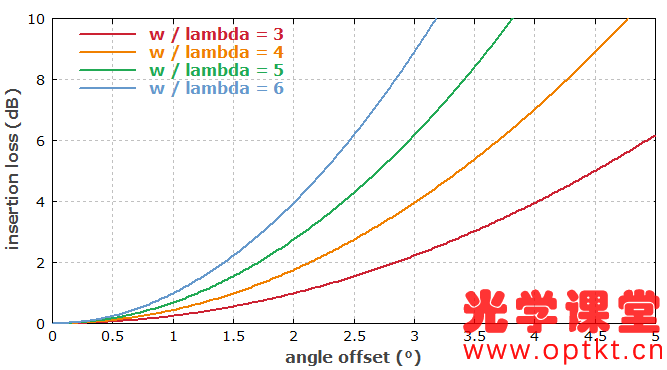
图4:由于由于角度误差,单模光纤机械接头处的插入损耗,这可能是由于非垂直切割造成的。这已经针对模式半径与波长的不同比率进行了计算。
关于角度切割光纤末端,切割角度需要多大才能避免显着反射到纤芯模式中这通常是令人感兴趣的。该等式可以很好地用于此;只需记住反射光束的角度偏差是切割角的两倍。例如,标准模式面积为 100 μm 2 且 w = 5.64 μm 的光纤需要至少 7.4° 的切割角,以便具有低于 10 -4 的背反射,即至少 40 dB 的回波损耗,在 1.5 μm 波长处。对于1000 μm 2 的大模面积光纤, 2.3° 就足够了。请注意,较长的波长需要较大的切割角,因为它们会导致较大的光束发散。
但是请注意,上述方程仅对具有高斯分布的模式有效。然而,在从成角度的光纤末端高度抑制背向反射的情况下,结果对与高斯模式分布的偏差很敏感。在那里,人们必须根据计算出的模式分布数值计算背反射,例如使用我们的 RP Fiber Calculator PRO 软件。
考虑更多细节很有趣。例如,如果模式尺寸不同,输入光来自哪根光纤的损耗是否重要?根据上面的公式,它没有。这是事实,尽管可能令人惊讶:可以想象,从较小的磁芯到较大的磁芯会导致比在另一个方向上更低的损耗。但是请注意,较小的模式具有较大的光束发散角,即空间傅里叶空间中的场分布较宽,这对于具有较大模式的其他光纤来说太大了。因此,在接头处损失的功率比例实际上并不取决于方向。只有丢失的光在包层模式上的分布不同。
可以想象,当从较小模式的光纤转换到具有较大模式的光纤时,如果第二根光纤具有相同的 NA(尽管纤芯较大),则可以避免耦合损耗。(如果 V 数足够低,它可能仍然是单模。)毕竟,角度范围应该仅受 NA 限制。然而,这种期望是错误的;如果两根光纤都是单模光纤,那么模式尺寸的不匹配不可避免地会导致耦合损耗。
多模光纤
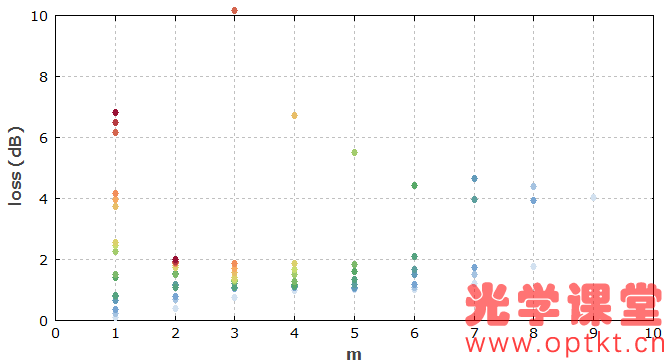
对于多模光纤,不能将损耗指定为单个数字:它们通常与模式有关。这意味着对于任意输入光场,所产生的总损耗将取决于功率在模式上的分布方式。例如,人们可以想象,光只能通过激光发射到低阶模式,这会导致低熔接损耗。如果在熔接前强烈弯曲光纤,光可能会重新分配到高阶模式,熔接损耗会变大。
以耦合损耗为例,考虑两个阶跃折射率多模光纤之间的完美机械接头,其 NA 相等,为 0.2(根据最大折射率差计算),但第一根光纤的纤芯直径为 62.5 μm,而第二根光纤的纤芯直径仅为 50 微米。我们可以计算第一根光纤的每个模式,将其与第二根光纤的所有模式的重叠积分的模量平方相加,从而得到其耦合损耗。(或者,可以使用数值模拟的光束传播,但这需要更多的计算时间并且暂时不太精确。)图 2 显示了损耗与模式的 m 值的关系。对于低m但高l值,这些损失最高。