激光

RP系列 | 如何计算激光谐振器中的失调效应

2021-05-06 11:45发布

站内文章 / 激光
725 0 0

        在实际的激光谐振腔设计中，必须考虑谐振腔镜对不对准的灵敏度。这里，解释了如何计算灵敏度，并在数值优化中加以考虑。

在分析谐振腔设计时，通常假定谐振腔是完全对齐的。然而，分析失调效应也很重要——特别是在开发商业产品时。

基础知识

 最重要的不对准类型是镜面的角度朝向与其标称位置的偏差。这不仅是由于主动转动镜面支架上的螺丝，而且由于热效应也很容易产生。特别是对于模区相对较大的激光器，微小的角度失调会导致实质性的影响。本质上，谐振器的模态将从它们的正常位置移开，从而再次以完全垂直的方式击中端面镜。(这里我总是假设一个线性谐振器，这是最常见的。)即使这些模式与所有镜面的边缘保持足够的距离，从而避免了这些边缘的衍射损失，问题通常是减少了激光晶体中泵浦光和激光束的重叠。这不仅会降低输出功率，而且常常还会降低光束质量。

优化重要性

有趣的是，激光谐振腔的对准灵敏度可以敏感地依赖于各种参数，当操作点通过激光晶体的热透镜改变时，它会发生强烈的变化。典型地，一个线性谐振器有两个稳定区域，在这两个区域的对准灵敏度可能非常不同;甚至在四个稳定边缘之一的对准灵敏度有一个发散，在这一点附近操作激光器是不可取的。
你可以看到，对齐灵敏度真的取决于设计，而不仅仅是一些基本参数，如谐振器长度和模态尺寸。

计算方法

对于简单谐振器，根据简单的几何考虑计算光束位置的位移并不太难。这将很快变得不方便，例如，如果在激光晶体中有几个曲面镜和/或热透镜。自然的解决方案是，用于谐振器设计的软件不仅计算光束半径，而且计算这种不对准效应。下面，我简要解释一下它是如何工作的。
仅对于电子束半径的计算，人们通常使用所谓的ABCD矩阵。这些最初是为纯粹的几何设计考虑在射线光学,后来发现是非常有用的波动光学，这样一个矩阵不能只适用于几何向量,也用于传播所谓的复杂的q参数的高斯光束携带信息的光束半径和波前曲率梁。
然而，这对于不对齐计算来说是不够的。为此，这种方法必须加以扩展:我们可以使用所谓的 ABCDEF 矩阵(o.e. Martínez，“色散激光腔的矩阵形式主义”，J.Quantum Electron. 25(3)， 296(1989))，它包含两个额外的参数E和F，这两个参数与误差有关，除了一些常量成分。我们可以将3×3矩阵应用到包含光束偏移量、光束角度和“1”作为第三分量的几何3分量向量上，以便将失调传播到整个谐振器中。进一步，我们可以计算出一个特征向量，它在谐振器的一个往返行程后被复制;这给出了在失调情况下的模态位置。
我只是告诉你，技术细节非常复杂。我记得我花了很多时间在非常复杂的工作上，部分原因是上面的论文中的方程式出现了错误。当这最终成功时，我只在一篇发表的论文(J. Opt. Soc。点。B 17 (4)， 646 (2000)， doi:10.1364/JOSAB.17.000646)。然而，这个软件后来变得非常有用——不是为了最初的目的，而是为了解决通用谐振器的设计问题。它最终发展成为软件RP谐振器，RP Photonics 现在出售用户许可证。

与波长有关的光术问题

所描述的方法也可以应用于波长依赖性折射的影响。例如，考虑在锁模激光器中用于色散补偿的棱镜对。在这种情况下，循环超短脉冲的每个波长分量在谐振器的部分位置有些微不同的光束，而产生的波长依赖的路径长度产生色散。对于简单的棱镜对，我们可以使用特定的公式来计算产生的色散，但如果软件能够计算出任意谐振器的这种影响，那就很好了。例如，我们也可以考虑到布鲁斯特界面的折射效应。

如何正确的使用软件

当你有软件RP谐振器，计算失调效应变得相当容易。它只需要两件事:
对于那些错位的谐振镜，指定角误差，附加参数为切向的delta_t或矢状方向的delta_s。
使用函数d_t()和d_s()，例如，绘制从标称波束位置的切向和矢状波束偏移量作为z位置的函数。(对于angular的偏移量，还有da_t()和da_s()函数。)

下面你可以看到一个典型激光谐振器的例子(见黑色虚线曲线)。对准灵敏度在左稳定边缘发散，在右稳定区域小得多。在实践中，你会发现在低泵浦功率下谐振腔是很难对齐的。在其他情况下，它是反过来的，例如，随着泵功率的增加，发散对准灵敏度。显然，在你决定建造共鸣器之前，你想知道这些!


图片

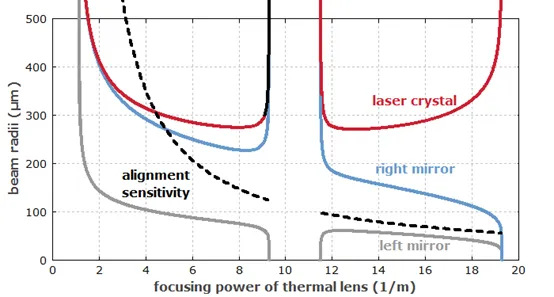
图1:激光谐振腔热透镜聚焦功率(与泵浦功率成正比)变化的稳定区。实线表示光束在不同位置的半径，虚线表示当输出耦合器倾斜1 mrad时，光束在激光晶体处的水平偏移量。

您可以将这些功能用于绘图。例如，对于谐振腔设计的数值优化，您可以定义一个包含对准灵敏度的品质因数函数。在激光晶体中，还可以定义由于未对准而导致的光束位置的灵敏度而发生数值偏差。

赞赏支持

热门文章